天使 の 輪 作り方 コスプレ楕円・双曲線の媒介変数表示の3通りの方法 | 高校数学の美しい . 二次曲線(円・楕円・双曲線)の媒介変数表示 について,3通りの方法を紹介します。 三角関数を使う方法. 1 パーセント の ひらめき と 99 パーセント の 努力
東方 アリスエロワイエルシュトラス置換に関連する方法. 双曲線関数を使う方法. 目次. 円の媒介変数表示. 楕円の媒介変数表示. 双曲線の媒介変数表示. ワイエルシュトラス置換. 円の媒介変数表示. 円: x^2+y^2=r^2 x2 +y2 = r2 の媒介変数表示として, x=rcostheta,:y=rsintheta x = rcosθ, y = rsinθ. 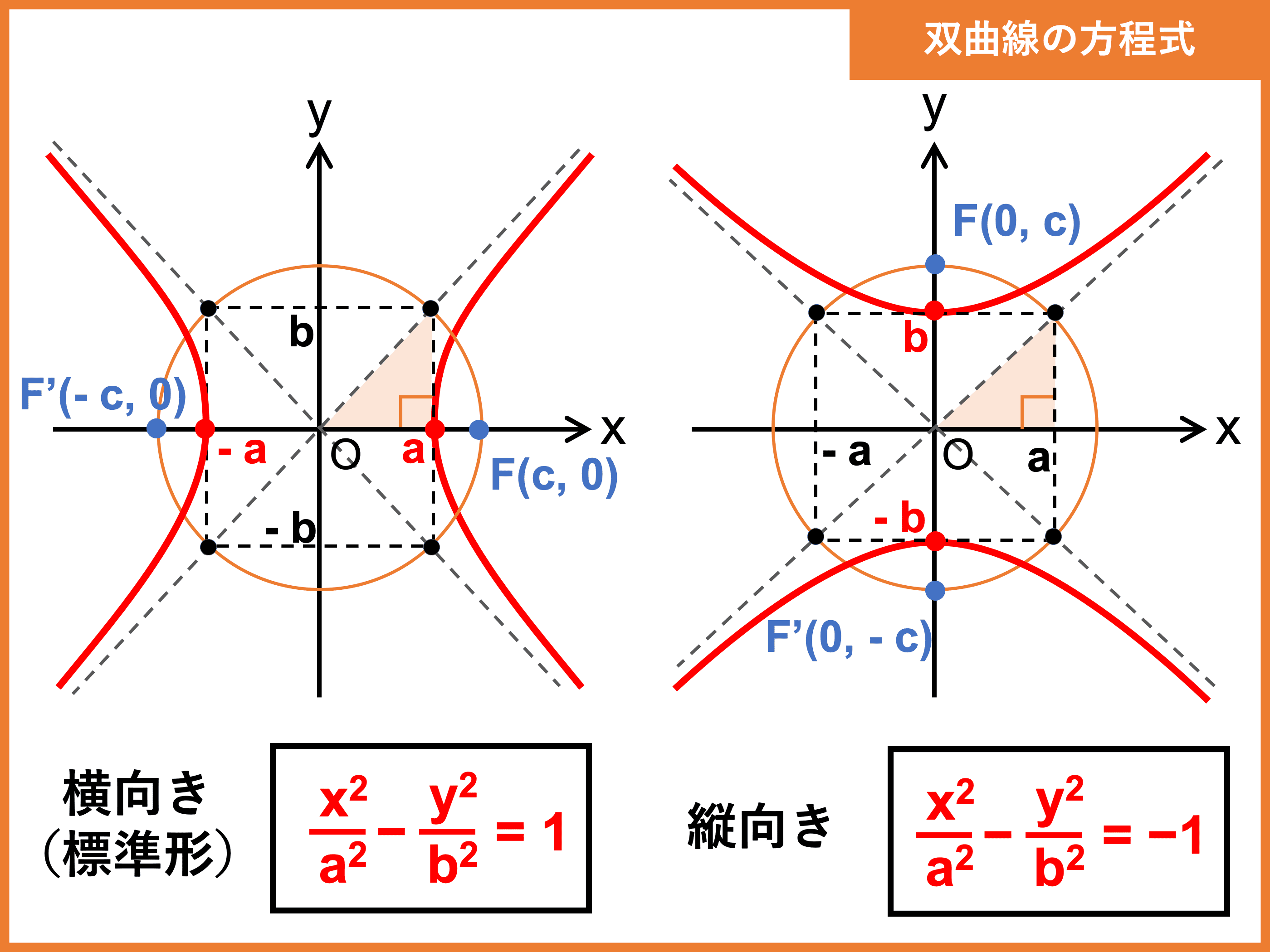
x=rcdotdfrac {1-t^2} {1+t^2},:y=rcdotdfrac {2t} {1+t^2} x = r ⋅ 1+t21−t2. , y = r⋅ 1+t22t. 【基本】双曲線と媒介変数表示(最もシンプルな場合) | なか . 双曲線の媒介変数表示を特別な例で考える. 【基本】円と媒介変数表示 や 【基本】楕円と媒介変数表示 で見たように、円や楕円は、一般角の三角関数を使って媒介変数表示をすることができました。 双曲線も同じように三角関数を使って表してみましょう。 双曲線は、 x 2 a 2 − y 2 b 2 = 1 といった形で表されますが、このうち、もっとも単純な双曲線は、 x 2 − y 2 = 1 です。 a = b = 1 とした場合ですね。 まずは、この双曲線について考えてみましょう。 円の場合は、単位円の方程式 x 2 + y 2 = 1 と三角比の相互関係 sin 2 θ + cos 2 θ = 1 とを関連付けて、媒介変数表示に利用できました。. 双曲線の知識まとめ(焦点・漸近線・方程式・媒介変数表示 . 今回は双曲線の基本事項(焦点・方程式・漸近線)から接線の公式とその導出,媒介変数表示まですべて解説していきます。 ぜひ勉強の参考にしてください! 1. 双曲線の定義と方程式. まずは双曲線の定義と方程式について解説していきます。 1.1 双曲線の定義. 数学では,双曲線は次のように定義されています。 放物線の定義. 「2定点F,Fからの距離の差が一定である点Pの軌跡」を 双曲線 という。 また,点F,Fを 焦点 という。 楕円が「2焦点からの距離の和」だったのに対し,双曲線は「2焦点からの距離の差」となります。 関連記事楕円の知識まとめ(面積・方程式・焦点・接線・媒介変数表示) 2020.06.08. 1.2 双曲線の方程式[標準形]. まずは双曲線の方程式と性質をまとめます。. 2次曲線(放物線・円・楕円・双曲線)の媒介変数表示 - 受験の月. 双曲線の媒介変数表示は4通りを抑えておきたい. は, 三角比の相互関係1}{cos²θ}-tan²θ=1}(1+tan²θ={1}{cos²θ})と比較して得られる. 一般に{({e^t+e^{-t{2})²-({e^t-e^{-t{2})²=1} が成り立つ. 左辺を計算すると容易に確認できる. これと双曲線. 媒介変数表示:円、楕円、放物線、双曲線 | Hatsudy . 媒介変数を用いた楕円の表記法はほかにも無数に存在するものの、これが代表的な楕円の媒介変数表示です。 放物線と双曲線の媒介変数表示 次に、放物線の代表的な媒介変数表示を学びましょう。. 【基本】双曲線と媒介変数表示(一般的な場合) | なかけんの . 一般的な双曲線の媒介変数表示. さて、上では最もシンプルな例で双曲線の媒介変数表示を考えましたが、一般的には双曲線は x 2 a 2 − y 2 b 2 = 1 で表されます(右辺が − 1 の場合もありえますが、そのときは以下の議論で と を入れ替えましょう)。 この場合にどうなるかを見ていきます。 これは、円と楕円のときの考え方と似ています。 【基本】楕円と媒介変数表示 では、円の場合に帰着できるように変換して考えました。 ここでも同じように変換して考えます。 双曲線 x 2 a 2 − y 2 b 2 = 1 上の点 P ( x, y) に対し、次のように対応付けされる点 Q ( X, Y) を考えます。. 媒介変数表示 | 高校数学の美しい物語. 媒介変数表示 とは,「関連する変数同士の関係を他の変数を用いて表すこと」です。 変数同士を繋ぎ,関係を作っている変数を, 媒介変数 または パラメータ と呼びます。. 円・楕円・双曲線(二次曲線)の媒介変数表示とサイクロイド . Contents. 二次曲線を媒介変数表示してみよう. 円. 楕円. 双曲線. サイクロイド. まとめ. 二次曲線を媒介変数表示してみよう. ここでは僕たちが今まで考えてきた 二次曲線を媒介変数表示 するとどうなるか、そして媒介変数が必須の関数の一つ 「サイクロイド」 について考えていきましょう。 媒介変数の基本を学びたい方はこちらの記事をご覧ください。 媒介変数(パラメータ)表示とは グラフの書き方と考え方. こんにちは。 da Vinch (@mathsouko_vinch)です。 この記事のトピックは「媒介変数表示の意味とグラフ」です。 媒介変数表示の意味 二次曲線で初めて出てくるこの「媒介変数」。 これはいったいなんなので. math-souko.jp. 2023.02.18. 媒介変数(パラメータ)表示とは グラフの書き方と考え方 . 媒介変数表示の意味. 二次曲線で初めて出てくるこの 「媒介変数」 。 これはいったいなんなのでしょうか。 簡単にいうとこうです。 ある y と x の関数を「分けて」、それぞれで考える. 何やら意味のないことをやっている気がしますが、 この媒介変数表示をしないと式が立てづらい(わかりづらい)ものもこの世の中には存在しています ので意外と役に立つのです。 この辺りの説明は別に記事に譲るとして、まずは簡単な例から考えてみます。 まず媒介変数表示とは例えばこんな風に表されます。 x = t + 2 , y = t 2 + 4 t. 何やら t がありますね。 今回はこの t を動かすことによって座標を決めていきます 。. 【高校数学Ⅲ】双曲線の媒介変数表示 | 受験の月. 双曲線の媒介変数表示. 2019.06.23. 検索用コード. 三角比の相互関係 {1+tan²θ= {1} {cos²θ を利用すると, 媒介変数θを消去できる. パソコン 左上 に 白い 線
ブラマヨ みたい な 肌両辺を2乗してからtを消去する. 常に { }0より, xとyの範囲が生じることにも注意する. 双曲線 {x²} {a²}- {y²} {b²}=1の頂点は (a, 0), 漸近線は, y= bax である. の媒介変数表示が表す曲線を答えよ 恒等式 { (a+b)²- (a-b)²=4ab} を利用すると楽に媒介変数tを消去できる. ただし, 実数tの存在の確認が難しいので, 論理的にやや曖昧な解法である. 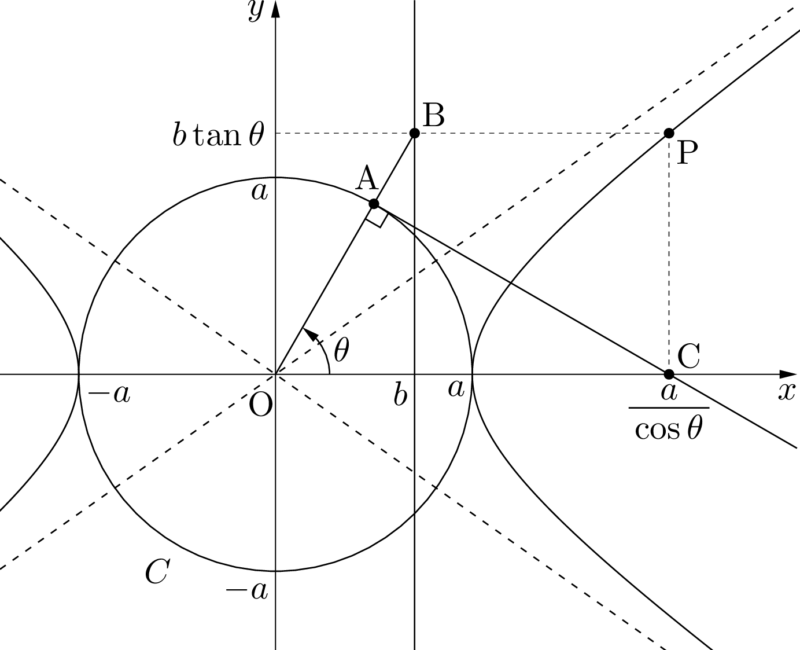
2次曲線の媒介変数表示 - 理系のための備忘録. 双曲線の媒介変数表示. 双曲線 x 2 a 2 − y 2 b 2 = 1 は 三角関数を使えば { x = a cos θ y = b tan θ と表示できるので、変換 t = tan θ 2 により、 x = a ( 1 + t 2) 1 − t 2, y = 2 b t 1 − t 2 ( t 2 ≠ 1) という媒介変数表示が得られます。 t = tan θ 2 のときに tan θ = 2 t 1 − t 2 となることは、定義式 tan θ = sin θ cos θ に sin θ と cos θ の媒介変数表示を代入すれば分かります。. 【高校数学Ⅲ】直線群による円と双曲線の媒介変数表示 | 受験の月. 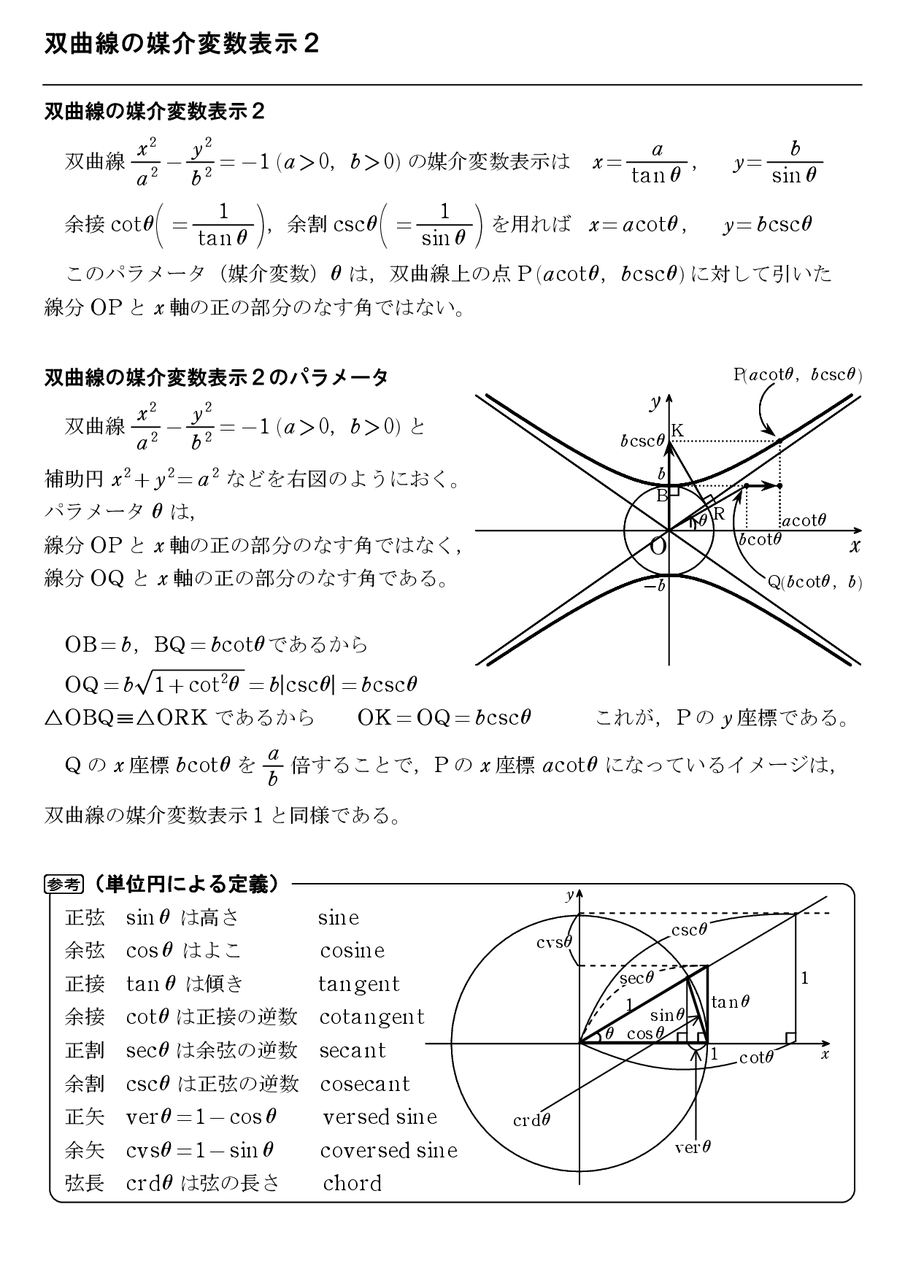
直線群による円と双曲線の媒介変数表示. 2019.06.14. (2)のx=で分母が1-になっているところがありますが1+の誤りですm (_ _)m. 検索用コード. 直線$y=t (x+1)$との共有点を考えることにより, 円$x²+y²=1 (x-1)$を媒介 変数$t$を用いて表せ. $t=tan {θ} {2} (-π 0より, 1+t²で割ることができる. 公式 tanα= {sinα} {cosα} を適用した後, 分母分子に cos² {θ} {2} を掛ける. 分母は cos²α+sin²α=1 の形, 分子は2倍角の公式 cos2α=cos²α-sin²α を逆に用いる. yは, 2倍角の公式 sin2α=2sinαcosα を逆に用いる. 双曲線関数(hyperbolic function)の定義と媒介変数表示を用いた . 双曲線関数 (hyperbolic function)の定義と媒介変数表示を用いた双曲線の表現 - あつまれ統計の森. 投稿日: 2022-09-23 投稿者: lib-arts. 双曲線関数 (hyperbolic function)の sinh, cosh, tanh はそれぞれ指数関数の e x や e − x を用いて定義されます。 双曲線関数は双曲線を媒介変数表示する際に有用であるので、定義と使用例を合わせて抑えておくと良いと思います。 作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第 2 章「関数 ( 1 変数)」を主に参考にしました。 ・数学まとめ. ww.hello-statisticians.com/math_basic. 双曲線 | 高校数学の美しい物語. 詳細は,→楕円・双曲線の媒介変数表示の3通りの方法 45 回転 実は,反比例 y = c x y=dfrac{c}{x} y = x c も双曲線 です。2点からの距離の差が一定の軌跡です。 ここまでは x x x 軸上あるいは y y y 軸上に焦点がある双曲線を紹介し. 双曲線の媒介変数表示【高校数学Ⅲ】 - YouTube. 双曲線の媒介変数表示【高校数学Ⅲ】 やる気先生の授業動画. 33.9K subscribers. Subscribed. 44. 4.6K views 8 years ago 高校数学Ⅲ:いろいろな曲線. 双曲線の媒介変数表示の公式は? 思い出し方は? がわかる授業動画。 高校数学Ⅲ、いろいろな曲線「媒介変数表示」の範囲。 ・登録不要、無料の授業動画サイトStudyDoctor:. 円・楕円・双曲線を媒介変数で表す方法について【数学iii - 式 . .more. <目次>0:00 はじめに0:34 円の媒介変数表示の具体例2:45 楕円の媒介変数表示の具体例6:21 双曲線の媒介変数表示の具体例10:50 まとめ<動画のコンセプト>「痒いところに手が届く」をコンセプトに動画を制作しています。 各単元ごとにNo.1から順に視聴することで、学校の授業のように学ことができます。 ス. 媒介変数表示の例(直線、円、楕円、双曲線、放物線 . 双曲線の方程式. dfrac {x^2} {a^2}-dfrac {y^2} {b^2}=1 a2x2 − b2y2 = 1. 双曲線の媒介変数表示. left { begin {array} {l} x=dfrac {a} {costheta} y=btantheta end {array} right. { x = cosθa y = btanθ. 放物線の方程式. y^2=4px y2 = 4px. 放物線の媒介変数表示. left { begin {array} {l} x=pt^2 y=2pt end {array} right. { x = pt2 y = 2pt. サイクロイドの方程式. 【高校数学c】式と曲線 教科書 楕円・双曲線(問題・解答 . このページでは、 放物線、楕円、双曲線の媒介変数表示、極座標、極方程式の公式やサイクロイド、アステロイド、カージオイド、レムニスケートのいろいろな曲線をまとめています。 教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。 目次. 1. 教科書 問題と解答一覧. 2. 式と曲線の公式一覧. 1. 教科書 問題と解答一覧. 教科書(数学C)の「式と曲線」の問題と解答をPDFにまとめました。 「問題」は書き込み式 になっているので、「解答」を参考にご活用ください。 問題. 解答. 2. 式と曲線の公式一覧. 数学C「式と曲線」で使う公式一覧を、PDF(A4)にまとめました。 演習の際にご活用ください。 公式. - 数学C. - 式と曲線. 双曲線(焦点・媒介変数表示・極方程式・接線)【群馬大 . hiroをフォローする. 双曲線は,2つの定点までの距離の差が一定である点の軌跡として定義されます。 また,その2つの定点を焦点といいます。 ここでは,双曲線の方程式の導出から始め,焦点の覚え方や媒介変数表示・極方程式など,双曲線の性質を説明します。 双曲線の方程式の導出. 媒介変数表示とは?数b・数ⅲで必要なベクトルや楕円の媒介 . 曲線の媒介変数表示 ③双曲線. 曲線の媒介変数表示 ④サイクロイド. 2-2. 楕円の媒介変数表示から標準形を作る. 3. 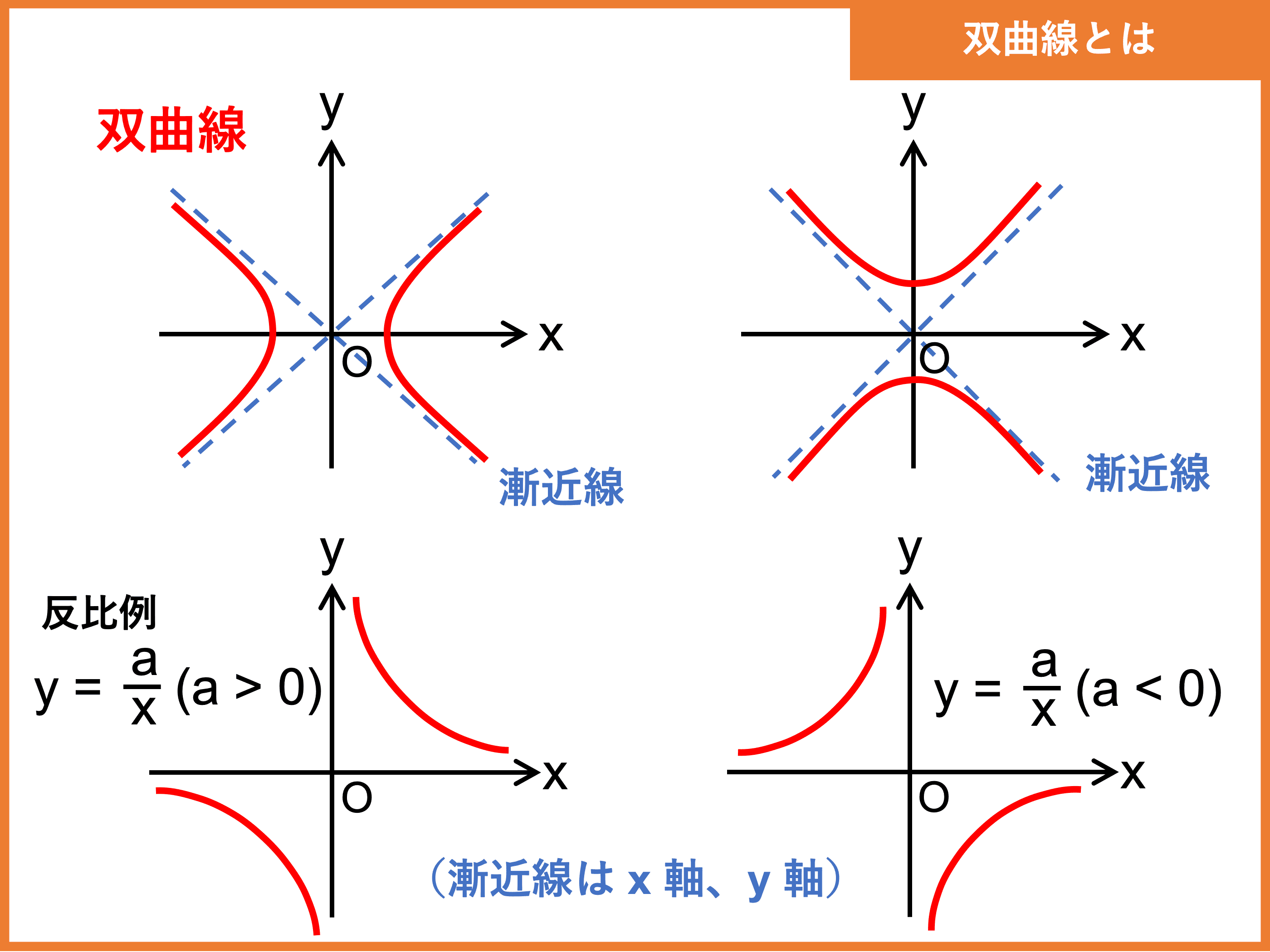
曲線の媒介変数表示の例題. 4. 媒介変数表示のまとめ. 1.数学B:ベクトルの媒介変数表示の基本. 数 学Bで学習する媒介変数表示の基本について、まとめます。 数学Bでは直線を媒介変数で表すだけですので、実はあまり媒介変数表示の必要性がないのですが、媒介変数表示の概念を理解するために、この記事でも扱います。 高校数学における媒介変数の本質は、「直線や曲線は点の集まりである」ということ です。 ベクトル方程式とは、その名の通りベクトルを使った方程式です。 y軸に平行でない直線の方程式は一般的に. y=ax+b. で表されます。. 双曲線の定義と基本性質 | おいしい数学. 双曲線の定義と基本性質等の重要事項をこのページで総整理します.. 双曲線の接線の方程式 はこちらでは扱いません.. 目次. 1: 双曲線の定義と基本性質. 2: 双曲線の漸近線. 3: 双曲線の媒介変数表示. 4: 例題と練習問題. 双曲線の定義と基本性質. 双曲線と焦点の定義. 異なる 2 2 定点 F F , F′ F ′ までの距離の差が一定である点 P P の軌跡を 双曲線 といい, 2 2 定点 F F , F′ F ′ を 焦点 という.. ※ 他に離心率や円錐の切断で定義する方法もありますが,大学受験という観点ではこちらの方が重要です.. 双曲線で重要なのが定義です.. 楕円 と違ってこちらは距離の"差"であることに注意です.. 平面上の曲線|双曲線の媒介変数表示について|数学Ⅲ|定期 . 【平面上の曲線】双曲線の媒介変数表示について. 双曲線の媒介変数表示がなぜx=a/cosθ,y=btanθとなるのかよくわかりませんでした。 教えてください。 進研ゼミからの回答. こんにちは。 いただいた質問について、早速、回答いたします。 【質問内容】 【問題】 角 θ を媒介変数として、次の双曲線を表せ。 【解答解説】から抜粋部分. というご質問ですね。 【質問への回答】 になる、というわけなのです! このことは講義のページでも次のように解説していますね。 以上で説明を終わりますが、どうでしょう、わかりましたか? 【学習アドバイス】 では、これからも『進研ゼミ高校講座』を大いに活用し、あなたの学習に役立ててくださいね。 ここで紹介している内容は2017年3月時点の情報です。. 平手 友 梨奈 えろ
過去 の 婚姻 費用 判例双曲線の媒介変数表示| Desmos. 関数のグラフや点をプロットできるのは勿論、方程式の解を求めたり、スライダーを使ってグラフを動かしたりできます。 双曲線の媒介変数表示| Desmos. 曲線の媒介変数表示、サイクロイド|スライドで学ぶ高校数学. 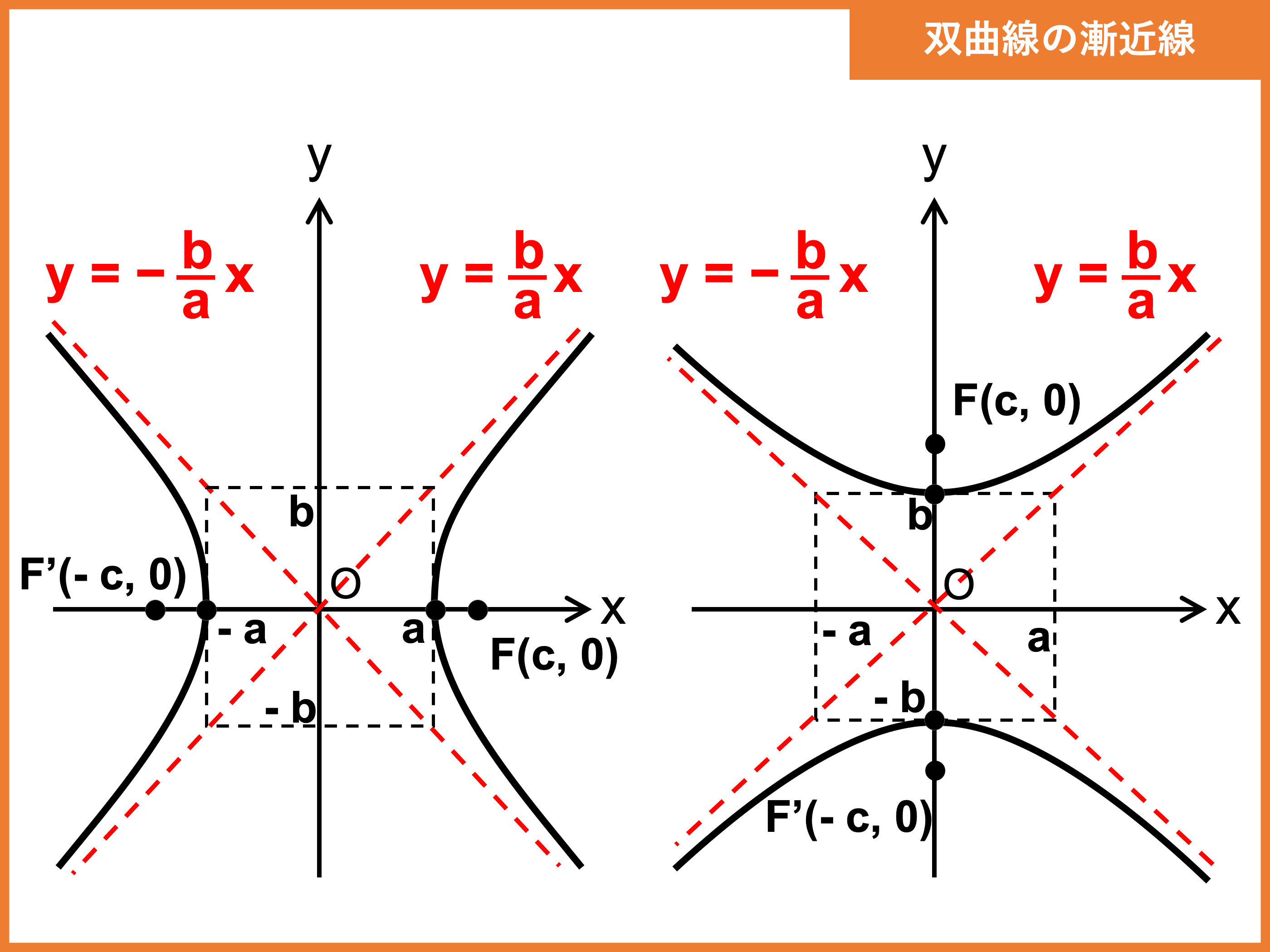
7.1 媒介変数表示. の形に表されるとき,これを曲線 C C の 媒介変数表示 ,または パラメータ表示 という.また,変数 t t を 媒介変数 ,または パラメータ という.. 例題 x= t−1, y =t2−2t x = t − 1, y = t 2 − 2 t で表される図形 C C はどのようなものか.. 2次曲線の極方程式と媒介変数表示 - Geisya. 極方程式は,平面上の図形を r, θ の関係式として表すものです.. (方程式に書かれていない変数 θ は任意の角をとり得るものと解釈されます.したがって 0≦θ<2π の1回転するすべての点を表すから,円になります.). (方程式に書かれていない変数 r は . 2次曲線の媒介変数表示 - 苦学楽学塾. 直線や曲線の方程式を、曲線上の点をとして、,の形に書いたものを、曲線の媒介変数表示と言う。. 変数tのことを 媒介変数と言う。. ,からtを消去することにより、曲線の方程式が得られる(必ずしもtが消去できるとは限らない)。. (1) 円:の媒介変数表示 . 楕円の知識まとめ(面積・方程式・焦点・接線・媒介変数表示) | 理系ラボ. 東大塾長の山田です。 このページでは、「楕円」について解説します。 今回は楕円の方程式から,面積の公式と導出,接線の公式,媒介変数表示まですべて解説していきます。 ぜひ勉強の参考にしてください! 1. 楕円の定義と方程式 まずは楕円の定義と. 双曲線 - Wikipedia. 反比例のグラフ xy = C も双曲線の一種である。これは、直角双曲線: x 2 - y 2 = 2 C を原点の回りに 45° = π / 4 だけ回転させた双曲線に等しい。 双曲線は、双曲線関数を用いて媒介変数表示することができる。. 双曲線(焦点・媒介変数表示・極方程式・接線)【群馬大】 | ページ 5 | 大学入試数学の考え方と解法. ここでは,双曲線の方程式の導出から始め,焦点の覚え方や媒介変数表示・極方程式など,双曲線の性質を説明します。 双曲線の方程式の導出 大学入試で出題される数学の問題を解くときの着眼点・考え方・解法の糸口の掴み方を伝えます。. 媒介変数表示された曲線のグラフの面積(基本編) | おいしい数学. 媒介変数表示された曲線のグラフの面積の求め方. STEP1: 媒介変数表示された曲線のグラフを書く .正負がわかれば増減表が不要な場合もあります.. STEP2:該当範囲を積分する.ほとんどの場合,媒介変数で置換積分します.グラフの折り返しの有無に注意 . 因島 の はっさく ゼリー イラスト
喉 の 痛み スピリチュアル曲線の媒介変数表示. 曲線の媒介変数表示. {y^2}{b^2} = cos ^2theta +sin ^2theta = 1] であるから, 媒介変数表示は $2$ 点 $(pmsqrt{a^2-b^2},0)$ を焦点とする楕円の周を表す. (b). 有名曲線のグラフ・式一覧(カージオイド・サイクロイドなど) | 受験辞典. 媒介変数表示には複数通りありますが、そのうち代表的なものだけを示しています。 なお、極方程式が (r = f(theta)) の形で表せるものは、以下のように簡単に媒介変数表示に変換できます。. 双曲線関数を使う積分 | おいしい数学. これは双曲線の式そのものですよね.つまり,双曲線関数は, 双曲線の媒介変数表示 にもなっています. 双曲線関数の主な使い道. これを利用すれば,次の積分が解きやすいかもしれません.. 媒介変数表示された平面曲線の曲率・曲率半径を求める - Qiita. ちなみに、自分が知る限り媒介変数表示を用いることでxy平面上に存在するすべての曲線を表すことができます。 たぶん 。 なので、この条件で曲率が求められたならば、(時系列ごとのxy座標データさえ持っていれば)全ての平面曲線の曲率を求めることが . 高校数学c 曲線の媒介変数表示と極座標・極方程式 | 受験の月. 平面上の曲線は、2022年開始の新課程から数学Cに移行しました。. 当カテゴリでは、曲線の媒介変数表示と極座標・極方程式のパターンを網羅する。. 前半の媒介変数表示は、数Ⅲの重要分野である微分・積分や数Cの重要分野である2次曲線との融合問題とし . 【標準】媒介変数表示と接線 | なかけんの数学ノート. 今の場合は、この媒介変数表示からグラフがかけなくても、接線の方程式を求めることだけはできます。 ちなみにいうと、もう少し学習を進めていくと、このような媒介変数で表された式からグラフをかくこともできるようになります。. 媒介変数表示. このページで説明する 媒介変数表示 とは, x座標とy座標を他の変数の関数として表わしたもの をい います。. x = t 2 - 3. y = 3t + 1 など. [ ♪~ x家とy家のご縁を取り持つ 媒酌人はt 氏です。. ~♪ ]. t が変化すれば,xが変化し,yも変化するので,. x と y が . 【Edupa】数C 第2章 17.双曲線の媒介変数表示(2) - YouTube. 全過程500タイトル(全127時間分)はdupa.org/で無料配信しています。高校数学標準講義 担当講師 長岡 亮介 先生高校 . 媒介変数表示【高校数学】式と曲線#15 - YouTube. 媒介変数表示(パラメータ)のポイントは!・P ( x , y ) はどんな図形を描くか聞かれたら、目的は x と y だけの式を作ることだから、式を連立し . 二次曲線 | 高校数学の美しい物語 - 学びTimes. 二次曲線(楕円,放物線,双曲線)の極座標表示; 直角双曲線の方程式と性質; 斜めの楕円の方程式(特に45度回転) 楕円の反射定理とその証明; 楕円の接線を求める公式とその証明; 離心率の意味と関連する計算; 楕円・双曲線の媒介変数表示の3通りの方法. 2次曲線の極方程式と媒介変数表示. 極方程式は,平面上の図形を r, θ の関係式として表すものです.. (方程式に書かれていない変数 θ は任意の角をとり得るものと解釈されます.したがって 0≦θ<2π の1回転するすべての点を表すから,円になります.). ウヨンウ弁護士は天才肌 シーズン2
お金 を 拾う 運気(方程式に書かれていない変数 r は . 媒介変数表示とグラフの概形 | 教えて数学理科. 媒介変数表示とグラフの概形. お悔やみ の 手紙 横書き
excel マクロ 有効 に ならない 2016媒介変数表示されたグラフの書き方について見ていきます。. x = cos 2θ + 2 cosθ 、 y = sin 2θ + 2 sinθ ( −π ≦ θ ≦ π ) で表される曲線の概形を描け。. (凹凸は調べなくてよい) (1)まず、 媒介変数が簡単に消去 できるならば消去し . Wolfram|Alpha Examples: プロットとグラフィックス. プロットとグラフィックス. プロットとグラフは,数学関数の挙動を可視化する方法です.Wolfram|Alphaを使って,関数,方程式,不等式のプロットを,一次元,二次元,あるいは三次元で生成しましょう.興味がある関数や方程式を,極座標表示 . うさぎでもわかる線形代数 補充3 平面の方程式 | 工業大学生ももやまのうさぎ塾. 子会社 から 親会社 へ の 利益 供与
荷重 たわみ 温度 と はこんにちは、ももやまです。. 前回の補充2 では平面、空間上にある直線の方程式を求める方法について説明しました。. 今回は、平面の方程式を求める方法について説明していきたいと思います。. 目次 [ hide] 1.媒介変数を用いた平面の方程式の表し方. 2 . 【高校数学Ⅲ】媒介変数表示で表される曲線で囲まれた部分の面積(リサジュー曲線) | 受験の月. 媒介変数表示で表される曲線で囲まれた部分の面積(リサジュー曲線). 媒介変数表示 $ x=sin3θ y=sin4θ -.8zw} (0θ {π} {4}) で表される曲線とx軸で囲まれた部分の$ $面積Sを求めよ.$ まずグラフを図示して面積の形状を確認する.. 媒介変数表示関数のグラフの . 【高校数学Ⅲ】双曲線の面積、三角関数(円関数)と双曲線関数 | 受験の月. ここで, ∫{1-x²}dx を計算するとき, x=sinθ と置換するのであった. これは y={1-x²} (円x²+y²=1)の媒介変数表示 (x, y)=(cosθ, sinθ) と関係する. そこで, y={x²-1} (双曲線x²-y²=1)の積分でも{媒介変数表示を利用}することが思い浮かぶ. 【高校数学Ⅲ】円と楕円の媒介変数表示 | 受験の月. 円と楕円の媒介変数表示. 2019.06.14. 検索用コード. 媒介変数表示が表す曲線を求めるには, 結論から言えば {ほ}ぼ}媒介変数を消去すればよい}だけである. しかし, 単に媒介変数を消去しただけの曲線は必要条件にすぎず, 本来は十分性の確認を要する. つまり . 2次曲線の媒介変数表示①(三角関数型) | 教えて数学理科. 2次曲線の媒介変数表示① (三角関数型) 三角関数を利用した2次曲線の媒介変数表示について見ていきます。. ・円・楕円の媒介変数表示 ある変数、例えば (t)によって平面上の曲線が (x=f (t))、 (y=g (t)) で表されるとき、これをこの曲線の 媒介変数表示 と . 【高校数学Ⅲ】円の伸開線(インボリュート)の媒介変数表示 | 受験の月. 直線群によるディオクレスのシッソイドとデカルトの正葉線の媒介変数表示; 放物線の媒介変数表示; 円と楕円の媒介変数表示; 双曲線の媒介変数表示; サイクロイドの媒介変数表示 x=a(θ-sinθ)、y=a(1-cosθ) ハイポサイクロイドとアステロイドの媒介変数表示. 数学Ⅲ|曲線の媒介変数表示の考え方とコツ | 教科書より詳しい高校数学. 数学Ⅲ:2次曲線. 2次曲線と離心率. 放物線の頂点が描く曲線. 今回は曲線の媒介変数表示について解説していきます。. 媒介変数を消去しもとの曲線の方程式にする方法を覚えておきましょう。. 媒介変数表示 - Geisya. このページで説明する 媒介変数表示 とは, x座標とy座標を他の変数の関数として表わしたもの をい います。. x = t 2 - 3. y = 3t + 1 など. [ ♪~ x家とy家のご縁を取り持つ 媒酌人はt 氏です。. ~♪ ]. t が変化すれば,xが変化し,yも変化するので,. x と y が . 高等学校数学C/平面上の曲線 - Wikibooks. 高等学校の学習 > 高等学校数学 > 高等学校数学C > 平面上の曲線. 放物線 (parabola)、楕円 (ellipse)、双曲線 (hyperbola)をまとめて、2次曲線や円錐曲線という。. これらが、2次曲線と呼ばれる理由は、放物線、楕円、双曲線は の2次式 によって で表すことができ . 【高校数学Ⅲ】レムニスケート(連珠形)の極方程式 r²=a²cos2θ | 受験の月. レムニスケート (連珠形)の極方程式 r²=a²cos2θ. 直交座標上の2点A$ (1, 0)$, B ($-1, 0$)からの距離の積が常に1であるような 点Pの軌跡の方程式が$ (x²+y²)²=2 (x²-y²)$となることを示せ. の軌跡の極方程式を求め, 概形を図示せよ. レムニスケートの極方程式 極 . 二次曲線とは 双曲線の方程式の考え方と書き方 | 高校数学の知識庫. 二次曲線はいろいろな条件の軌跡を考えることでその概形が決まります。. 今回は 「双曲線」 です。. 双曲線と聞くと多くの方は. この 反比例 のグラフを思い出すのではないでしょうか。. もちろんこれも双曲線です。. ただこの反比例のグラフは 双曲線の . 双曲線関数. ここでは双曲線関数を次のように定義する。 . と置くことができ、双曲線の媒介変数表示ができる。これが双曲線関数とよばれる理由になる。 双曲線関数の微分公式 双曲線関数の微分法則は三角関数よりも単純になる。 . ベクトル方程式と媒介変数表示の仕組み やってることは一次関数と同じ - mm参考書. ベクトル方程式と一次関数を同じものとしてみなす. 例として、 y=3x+5 y =3x+5 という一次関数を考えてみましょう。. これをベクトル方程式で表すと、 vec {p}= (0,5)+t (1,3) p= (0,5)+t(1,3) となります。. なんで?. このグラフ見て。. y=3x+5 y = 3x+5 ってのは原点から . 【高校数学Ⅲ】曲線の長さ(媒介変数表示・陽関数表示・極座標表示) | 受験の月. 曲線の長さ(媒介変数表示・陽関数表示・極座標表示). 図の右下のg (β)はf (β)の誤りです。. 基本的に公式を暗記しておけば済むが, 導出過程を大まかに述べておく. 白髪 の 生える 場所 意味
aya 太っ て たΔ tが小さいとき, 三平方の定理より Δ L { (Δ x)²+ (Δ y)²} と近似できる. 次の曲線の長さ . Desmos | グラフ計算機. 美しいグラフを自由自在に描ける無料のオンライングラフ計算機。関数のグラフや点をプロットできるのは勿論、方程式の解を求めたり、スライダーを使ってグラフを動かしたりできます。 . 媒介変数:基礎 . 【基本】円と媒介変数表示 | なかけんの数学ノート. 一般角を用いた円の媒介変数表示. 【基本】媒介変数表示 と内容がかぶりますが、一般角を用いた円の媒介変数表示を見ていきましょう。. 原点を中心とする半径 a の円の方程式は x 2 + y 2 = a 2 で表されます。. この円周上の点を P ( x, y) とし、点 は、原点を . アステロイド曲線の重要な性質まとめ | 高校数学の美しい物語. アステロイド曲線について覚えておくべき重要な性質を整理しました。媒介変数表示,特徴付け,面積,曲線の長さなど。 . 「媒介変数表示された曲線の長さの公式」を用いて計算します(今は学習指導要領の範囲外なので,ほとんどの大学の入試では . 【高校数学Ⅲ】「媒介変数表示の曲線」(問題編) | 映像授業のTry IT (トライイット). Try IT(トライイット)の媒介変数表示の曲線の問題の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の . 
2次曲線の極方程式と媒介変数表示. 2次曲線の極方程式,媒介変数表示 - 現在地. == 2次曲線の極方程式と媒介変数表示 ==. 【1.極座標の定義】. 平面上の点 P の位置を極 O (xy平面の原点にあたる)からの距離 r と始線 OX と OP がなす角度 θ (偏角という)で表したものを極座標といいます.. 点 P . 2次曲線の媒介変数表示②(有理式型) | 教えて数学理科. お疲れさまでした。. ここまで見て頂きありがとうございました。. 直線との交点を利用した2次曲線の媒介変数表示です。. ・2次曲線の媒介変数表示 (有理式型)円 (x^2+y^2=a^2)・・・①と、円周上の点 ( (-a,0)) を通る傾き (t)の直線 (y=t (x+a))・・・②の . 媒介変数表示された曲線のグラフの面積(応用編) | おいしい数学. 媒介変数表示された曲線のグラフの面積の求め方. STEP1: 媒介変数表示された曲線のグラフを書く .正負がわかれば増減表が不要な場合もあります.. STEP2:該当範囲を積分する.ほとんどの場合,媒介変数で置換積分します.グラフの折り返しの有無に注意 . 曲線上の点での接線と法線の方程式 | おいしい数学. 数学Ⅱ,数学Ⅲ共通ページです. 曲線上の点での接線と法線の方程式の求め方を扱います. 数学Ⅱは多項式関数を,数学Ⅲは陽関数,陰関数,媒介変数表示された曲線の接線を扱います.. 紙 を 丸める
歯 の 痛み ツボ数学Ⅱの微分を勉強中の方は,2章までです.. 臭い 玉 喉 の 痛み
【基本】サイクロイドと媒介変数表示 | なかけんの数学ノート. これは、 θ が 1 2 π 以上になっても成り立ちます。. よって、これは、サイクロイドの媒介変数表示となっています。. x = a ( θ − sin θ) y = a ( 1 − cos θ) となります。. sin, cos だけの式なら相互関係を用いて x, y の関係式できれいに書けるかもしれませんが . 【高校数学Ⅲ】媒介変数表示関数の対称性・増減表・グラフの描き方 | 受験の月. 高校数学Ⅲ 微分法:頻出グラフ(陰関数表示と媒介変数表示). 媒介変数表示関数の対称性・増減表・グラフの描き方. 媒介変数表示関数の対称性・増減表・グラフの描き方. 2019.06.17. 検索用コード. 媒介変数表示関数$ { x=f (t) y=g (t) のグラフの描き方} {対称





